![[The TNT Convertus]](../gif/convertus.gif)
![[The TNT Convertus]](../gif/convertus.gif)
A few months ago I decided to look hard for something in that area. I had just finished (well, kind of... my projects always tend to be a sort of never ending stories) a solid state RIAA design which, with the help of our friend Norbert, was quite a surprise for the kind of sound: half way between solid state and tubes... really interesting (it is our TNT Solidphono).
The result was that I started listening vinyl a lot and was no longer able to bear CD's sound; you know, just one of those dangerous relapses audio addicts are used to, especially after changing a component of their system: you go on listening to the better source you have, and cannot bear any other...
But even though you can find an economically acceptable source for second-hand vinyl, there is no point: vinyl is the past, CD is the present and other digital stuff will be the future.
Perhaps it does not sound so exciting to most of you, and I could well include myself in the list, but if you listen to a 30 years old record played for a long time on a very economical turntable you cannot deny that on any aspect, apart the ones only audiophiles care for, CD has been a HUGE step on.
You must take into account the fact that Hi-Fi addicts are only a thin slice of the market. So you cannot expect that large companies look too hard for this thin slice.
Little specialised companies could be interested in addressing this market, but have anyway no chance of creating a new, higher level standard if not supported by large ones, which obviously could not accept their own standard to be classified as the "lower quality" one.
So we audiophiles cannot expect anything more than the best you can get out of the mass product currently made available by technology.
What seems even stranger, indeed, is that several last generation DACs, even with high bits number and high sampling speed, does not sound so well as expected.
Apparently there are still big technical problems which have badly reduced the performance of objects which should have theoretically been far better than their predecessors.
So at present time you can find 24bit, 96ksps DACs which have practical performances only slightly better than old 20bit, 48Ksps DACs, and I think we'll have to wait a not so short time for them to reach the theoretical performance allowed by these Ics.
But is this the moment to present a DIY 20bit, 44.1Ksps DAC design, with oncoming DVD-A and SACD?
Well, here are quite a few things that must be taken into account, but all of them take me to say that the future of the new media does not appear, in my opinion, so brilliant at present time, and not so imminent.
And anyway, from my point of view, I definitely needed to get a better sound out of CDs. And now.
In the following I start going through digital signal theory in general (do not worry, I try to use the simplest approach) and then address the specific problems of a two box (transport + D/A converter) implementation. Finally I'll describe the design, which is inherently based on theory, but as you'll see does not directly address any of the issues: they are solved "inside" the ICs used, so that the design issues are all of another kind.
We can start from the beginning. The signal is stored, as anyone knows, on the CD in a digital format named PCM.
To obtain this format two different and theoretically independent processes have been applied to analogue signal: sampling, that is the process that extract from the continuous analogue wave-form its exact analogue value at a given time, and quantization, that is the process that converts each sample exact analogue value in a number.
In a similar way, the process that transforms the PCM data into an analogue signal can be decomposed into two different tasks: the conversion of samples from a number into an analogue value and the reconstruction of the continuous wave-form from the sequence of analogue values.
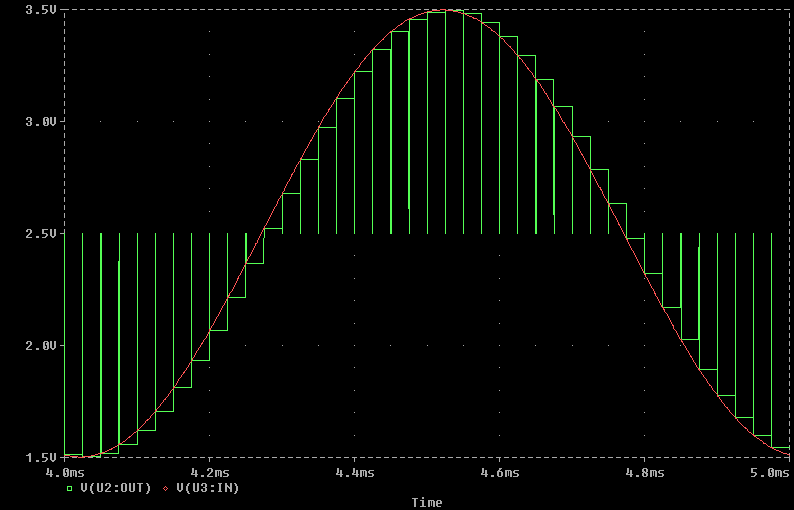
Fig.1
The fundamental theorem of digital signal processing (Shannon's Theorem) says that you can correctly reconstruct an analog signal from a sequence of samples of the same signal, provided that the maximum analogue signal frequency is no more than half the sampling rate.
This means that, under the hypothesis that there is no signal component at frequency higher than half of the sampling frequency (Fs = sampling frequency), the A/D-D/A conversion process theoretically does not loose any information. The Fn=Fs/2 frequency is called Nyquist frequency.
Note that the theorem does not take into account the way samples are stored: in facts it assumes that the samples value exactly matches the value of the original waveform at sampling instant, with absolute precision.
The theorem above anyway makes the usage of very steep low pass filters necessary both at A/D and D/A conversion time.
But why is this heavy filtering necessary at A/D conversion time? Well if you do not filter off all frequencies higher than half the sampling frequency, the D/A converter could reproduce the signal at (Fs/2 + K) Hz as a (Fs/2 - K) Hz signal, as it is not able to discriminate the two frequencies!
See in facts next diagram: two equal modulus sinusoids are represented, with the two frequencies over stated; as you can see, their value at sampling times (vertical lines) is absolutely the same, hence looking at
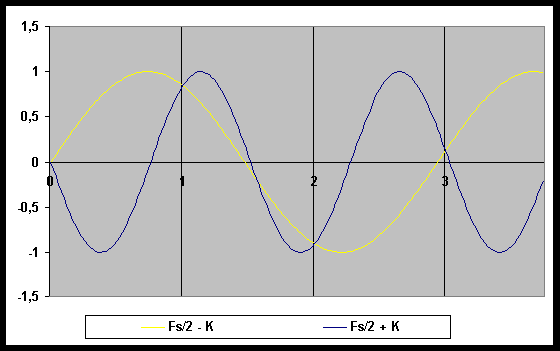
Fig.2
the only sampled values sequence it is not possible to discriminate between the two waveforms! This is the situation the Dac must cope with: there is no way to detect which is the original frequency, unless you can be sure that it is lower then Fs/2, which in turn can be granted only by ADC input signal filtering.
This effect is named aliasing: any input frequency between Fs/2 and Fs is made identical or translated by the sampling process into a frequency lower than Fs/2 (if the first one is Fs/2 + K then the resulting frequency is Fs/2 -K, as stated above) and vice versa; moreover any frequency higher than Fs, let's write it as Fs*N + H with H < Fs and N any value greater then or equal to 1, is made indistinguishable from the H frequency.
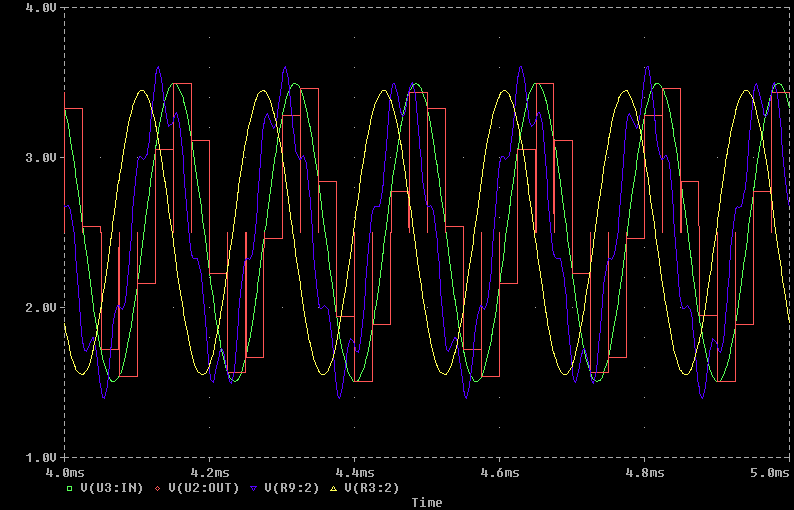
Fig. 3
An anti-aliasing filter is required after D/A conversion too. What happens is clearly shown in the simulation above. A 6KHz sinusoidal signal (green) has been passed on to a 12 bit/40Ksps ADC which converted it into a digital signal (not shown); the digital signal has been passed to a 12 bit/40Ksps DAC, which converts it back into an analog signal (red); the signal is then passed to two different low-pass filters, with a very sharp cut and a very high attenuation: the first one is a 20Khz low-pass filter, which is a theoretically correct anti-aliasing filter, and presents at its output (yellow) a correct reconstruction of the original signal; the second one is instead a 40KHz filter, which does not allows for a correct reconstruction: in facts the signal at its output (blue) is badly distorted. If you look at the spectral contents of this signal you can find a 34KHz (40-6=34) component which was not present in the original input signal, but has been generated during the A/D D/A conversion process by the aliasing effect.
The behaviour is really strange but its explanation, as we saw above, is really simple. Anyway, this causes great practical problems in CD audio reproduction, given the need for the widest possible band with a rather limited sampling frequency.
Another issue is the conversion precision. The Shannon's theorem (the one that says that you can always recover the original waveform from the sampled version provided that the highest signal frequency is less than Fs/2) does not take into account samples precision, which means that from its point of view each sample is the exact instantaneous value of the original waveform.
Any practical DAC, however, must face at least the fact that it is even theoretically not possible to store digitally infinite precision samples as this would require an infinite number of bits...
If you take into account the precision constraints imposed to chip design by a 16 bit integrated DAC it is immediately clear the dimension of the problem.
With regard to quantization, under a few special hypothesis (sinusoidal signal), the limited number of digits reduces theoretically the available dynamic to 6.02 * <n. of bits> dB.
Actually the A/D-D/A process precision is for sure limited by the number of bits available, but in general, given the different degenerative effects including linearity problems involved, is inferior to the theoretical value (however using special techniques is currently possible to obtain a precision superior to the theoretical one in a reduced range of frequencies, at the expense of a loss of precision in the other ranges).
Obviously these problems are well known and a few countermeasures have been studied.
The quantization error, that is the error the quantization process introduces in truncating to a given number of bits the representation of the original signal, can be normally seen as noise: this quantization noise is by the way the noise we compute using the 6.02*<n. of bits> equation.
In facts quantization error is one of the most important limiting factors in DAC behaviour. It limits DAC dynamics, but, what's even worse, if you take into account very low value signals, than the error introduce a very high distortion. For example, if a signal has a level slightly higher then the LSB (least significant bit) of the DAC, then the converted waveform will be a square wave only roughly similar to the original signal.
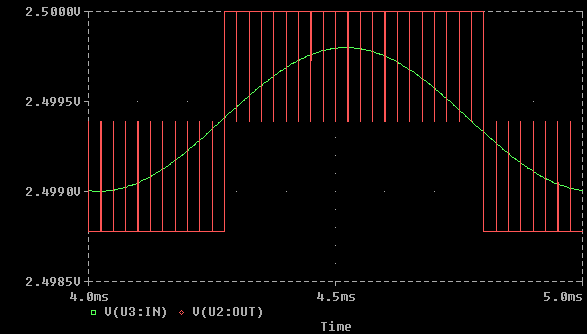
Fig. 4
The best solution studied to solve this distortion problem is to add some more noise to the input signal.
This high frequency random noise, named dither, is used to transform the original signal so that the single sample value is not more correct, but the squaring effect evident in the picture above disappears.
From the practical point of view, dithering decorrelates spurious conversion artifacts from signal, that is the distortion made apparent by the squaring effect is transformed by dithering into a random noise floor, which is anyway far less unpleasant to hear than the original distortion.
Moreover, dithering has also other good effects, for example helps in reducing the effects of DAC non-linerities, with a mechanism similar to the one above.
As we said before, the aliasing effect is so bad with CDs as the sampling frequency is so low, compared with the audio range : the audio range is up to 20Khz, and the Nyquist frequency is 22.050KHz.
This means that the first aliased image of the audio range just is placed between 24.100KHz and 44.100KHz: the analogue anti-aliasing filter must be extremely complex and expensive, with a very steep transition, as its pass band must end at 20Khz and its stop band begin at 24KHz, with a very high attenuation.
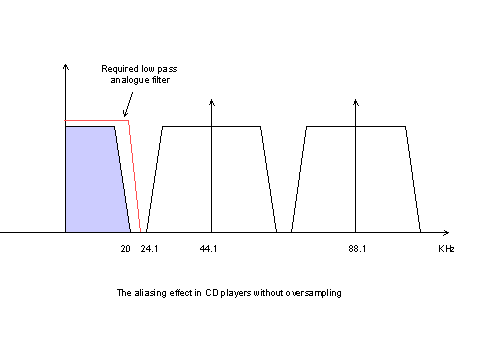
Fig. 5
One possible solution which is normally used is oversampling.
This originally should mean "to take much more then the necessary number of samples for a given time", but with the CD standard already defined it is obviously not possible to really record more samples.
Then the engineers add a number of null samples between any two 16bit/44.1Ksps original samples and then had this new digital signal to be processed by special low pass digital filters transition slopes not possible to implement with analogue filters, that are able to assign a correct value to the added samples.
At the output of these filters the signal is just a copy of the original one, but with a (far) higher sampling rate (e.g. 128 times higher then the original one).
This means that the aliasing effect is still present, and as usual the DAC output contains the first image of the audio range and all the aliased others, but now the first aliased image of the audio range appears at far higher frequencies than when no oversampling is applied, which in turn makes it possible to use low order low pass analogue filters.
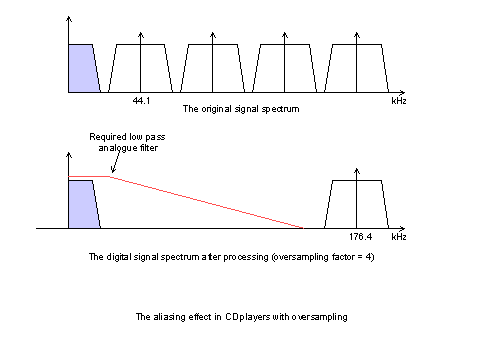
Fig. 6
Just to give an idea of the different possible implementations and just as a first approximation, we can say that there are different classes of D/A converters. Each class is subject to infinite detail variations, so that it is nothing more then a theoretical exercise.
The Red Book is the original CD standard document: it contains in principle any specification needed in order to grant that a CD can be read on any player. From our point of view we want to focus on sampling and quantization standard.
In case of audio CDs, each channel signal is represented by a different sequence of samples; each sample is an integer number of 16bit which contains the approximated instantaneous value of the signal at a specific time; in CD reproduction there are 44.1 Ksps, that is 44.1 thousand samples per second.
This means that S/N ratio should reach 96 dB and that the maximum frequency that can be correctly stored on a CD is just over 22KHz.
The reason for this numbers can be easily explained taking into account two facts.
On one side, as we have seen, there are the fundamental theorems of digital signal processing.
On the other side, 16 bit conversion at 44.1 sample rate was still rather beyond reach of existing technology when CD "Red Book" standard was defined: hence it was obvious to try keeping the sampling rate of the new low cost (don't forget...) medium as low as possible, provided that it would have been theoretically possible to reproduce correctly the full audio range up to 20Khz and over, with a dynamic of 96dB, which was typically higher than the LP one (well, here we assume the "technical" definition of dynamic, that is the difference between the highest and the lowest signal that can be reproduced, where the lowest value is typically limited by noise...).
Actually, there indeed is very few people who can hear up to 20Khz, and 96 dB of dynamics are really far more than necessary in a normal home environment, where the environmental noise is normally around 40dB, so that to be able to hear the lowest level details should require to reach 136dB (which is a just little less than the noise of a jet at taking off...).
But many of you can probably confirm that, while the CD player can sound really loud or really silent and has an outstanding intrinsic SN ratio, usually a CD player can produce an perceived impact much lower than a very good turntable one, and while the frequency response of a CD player is made perfectly flat, the sound is often less natural and I would say more coloured than the analogue one, where 0.5 dB is already considered acceptable (apart on Japanese, heavy feedback designs, where 0.05 or less is achieved...).
This means that theory is not perfectly applicable when hearing enters the play, or better that a more in depth analysis is required. It is well known, for example, that harmonics at frequencies higher than 20KHz, and hence "per se" not audible, can become audible by interacting with other signals.
Cutting away all frequencies over 22KHz, as MUST be done before A/D conversion at the recording site, for sure could modify the situation. Just to look at the same problem from another point of view, the sample flow is not continuous, that is not so short a time (22usec is quite a lot...) passes between a sample and the next.
In the meantime, please refer to Shannon to be reassured that you are loosing no meaningful information. Shannon could probably hear better than any audiophile... up to 22Khz, at least :-).
In the end the sampled and digitized signal is affected, even in theory, by a few problems: one is the fact that it has been cut down to 22KHz, the second is that the truncation of samples to 16 bits makes the precision and the detail not perfect, the third that as the aliasing is made evident in the D/A conversion process, at reproduction time another heavy low pass 22KHz filtering must take place.
Apart these problems, that cannot be directly addressed inside the "Red Book" standard (this is in facts the technical reason for DVD-A and friends), the sampled digital signal is recorded on the CD, with a lot of redundant extra bits in order to be reasonably sure that the original signal can be retrieved or reconstructed even when the surface is damaged.
Note that each one of the problems listed above have been addressed by different technical solutions which have solved them, at least from a technical point of view.
From a "sonic" point of view... well, I am not so sure the problem has been really solved...
Copyright 2000 Giorgio Pozzoli - https://www.tnt-audio.com
How to print this article